- ¿Qué son las pruebas Paramétricas?
- Requisitos para escoger una Prueba Paramétrica
- Guía paso a paso con Ejemplo
- ¿Por qué escoger una prueba paramétrica?
- ¿Cómo escoger la prueba paramétrica adecuada?
- Ventajas e inconvenientes de las pruebas paramétricas
- Entonces, ¿Cuál es la mejor prueba paramétrica?
- Resumen
- Preguntas Frecuentes
¿Qué son las pruebas Paramétricas?
Las pruebas paramétricas son pruebas que se utilizan en Estadística para analizar factores dentro de una población. Además, permiten cuantificar hasta qué punto dos variables son independientes o no lo son.
Este tipo de prueba asume distribuciones estadísticas subyacentes a los datos. Por tanto, deben cumplirse algunas condiciones de validez, de modo que el resultado de la prueba paramétrica sea fiable.
Requisitos para escoger una Prueba Paramétrica
Efectivamente, no siempre vamos a poder escoger una prueba paramétrica. Debemos asegurarnos de que se cumplen los siguientes requisitos en nuestra investigación:
Podría decirse que, en cualquier otra situación en la que no se cumplan estas condiciones, deberá usarse una prueba no paramétrica equivalente. Si no sabes a qué me estoy refiriendo, clica en el siguiente botón:
Guía paso a paso con Ejemplo
A veces, seleccionar una prueba u otra puede llevarte a un proceso abrumador. Para que eso no te pase, te he preparado un listado de todas las pruebas paramétricas más usadas en el TFG de Psicología con algunos detalles. Para que puedas escoger la que mejor te convenga según el ejemplo. Además, te las he ordenado en un orden que va de las pruebas más sencillas a las más complejas por dos motivos: para que intentes utilizar la más sencilla, en primer lugar, y que no cometas el error de planificar un análisis con una prueba realmente compleja que convierta tu experiencia del TFG en una pesadilla.
¡Tú tienes el mando!
Nivel de dificultad: básico.
Prueba t de Student
| Para 1 muestra | Utilizada para comparar la media de una muestra con una media poblacional conocida. Ejemplo: Verificar si la media de horas de estudio de una muestra de estudiantes difiere de la media poblacional de 5 horas. |
| Para muestras independientes | Ideal para comparar las medias entre dos grupos distintos. Ejemplo: Comparar el rendimiento académico (media de calificaciones) entre estudiantes de dos escuelas diferentes. |
| Para muestras emparejadas | Aplicada cuando se comparan las medias de dos grupos relacionados o medidas repetidas. Ejemplo: Evaluar el efecto de un programa de entrenamiento comparando los pesos de los participantes antes y después del programa. |
Nivel de dificultad: intermedio.
ANOVA (Análisis de Varianza)
| ANOVA de 1 factor | Cuando se investiga el efecto de una variable categórica sobre una variable dependiente continua entre tres o más grupos. Ejemplo: Analizar si hay diferencias en la ansiedad (variable dependiente) entre grupos de terapia distintos (variable independiente con tres niveles: cognitiva, conductual, y de relajación). |
| ANOVA de dos factores | Para estudios con dos variables independientes. Ejemplo: Examinar cómo el tipo de terapia (cognitiva o conductual) y el género (masculino o femenino) afectan los niveles de ansiedad, incluyendo la interacción entre género y tipo de terapia. |
Nivel de dificultad: avanzado.
Variantes del ANOVA
| ANCOVA | Para ajustar las diferencias entre grupos por variables adicionales. Ejemplo: Comparar el rendimiento académico entre tres métodos de enseñanza diferentes, ajustando por el interés inicial de los estudiantes en la materia. |
| MANOVA | Cuando el interés reside en cómo una o más variables independientes afectan a múltiples variables dependientes. Ejemplo: Evaluar cómo diferentes tipos de terapia afectan simultáneamente la ansiedad y la depresión. |
| MANCOVA | Similar al MANOVA, pero ajustando por covariables. Ejemplo: Investigar los efectos de diferentes programas de ejercicio sobre el peso y la presión arterial, controlando por la edad y el género. |
| ANOVA de Medidas Repetidas | Para datos donde las mediciones se repiten en los mismos sujetos. Ejemplo: Estudiar el efecto del tiempo (antes, durante y después) en la ansiedad de un solo grupo sometido a terapia. |
| ANOVA de Medidas Mixtas | Para análisis que involucran tanto medidas repetidas como comparaciones entre grupos. Ejemplo: Comparar la progresión del aprendizaje en matemáticas a lo largo del tiempo entre estudiantes que usan diferentes métodos de enseñanza. |
Pruebas Específicas Derivadas
| Prueba t de Welch | Para comparaciones de dos grupos con varianzas desiguales. Ejemplo: Comparar puntajes de satisfacción laboral entre dos departamentos de una empresa, asumiendo varianzas desiguales. |
| Regresión Lineal y Correlación de Pearson | Para modelar y analizar la relación entre dos variables cuantitativas. Ejemplo: Determinar la relación entre horas de estudio y rendimiento académico en estudiantes universitarios. |
¿Por qué escoger una prueba paramétrica?
Las siguientes razones podrían justificar el uso de pruebas paramétricas en una investigación determinada:
Funcionan muy bien para analizar datos con distribuciones asimétricas y no normales
Esto puede ser una sorpresa, pero las pruebas paramétricas pueden funcionar bien con datos continuos que no son normales si se cumplen las pautas relativas al tamaño de la muestra que se indican en la siguiente tabla.
| Análisis paramétrico (medias) | Pautas sobre el tamaño de la muestra para datos no normales |
|---|---|
| Prueba t de 1 muestra | Mayor que 20 |
| Prueba t de 2 muestras | Cada grupo debería ser mayor que 15 |
| ANOVA de un solo factor | 1) Si tiene de 2 a 9 grupos, cada grupo debe ser mayor que 15. 2) Si tiene de 10 a 12 grupos, cada grupo debe ser mayor que 20. |
Son muy adecuadas en caso de que haya dispersión diferente en cada grupo
Aunque las pruebas no paramétricas no presuponen que los datos siguen una distribución normal, sí tienen otros supuestos que pueden ser difíciles de cumplir.
Para las pruebas no paramétricas que comparan grupos, un supuesto común es que los datos de todos los grupos tienen la misma dispersión. Si los grupos tienen una dispersión diferente, las pruebas no paramétricas podrían no proporcionar resultados válidos.
Por otro lado, si utiliza la prueba t de 2 muestras o el ANOVA de un solo factor, simplemente puede ir al cuadro de diálogo secundario Opciones y desmarcar Asumir varianzas iguales. Voilà, ¡puede continuar aunque los grupos tengan dispersiones diferentes!
Detectan más fácilmente los efectos significativos
Las pruebas paramétricas suelen tener más potencia estadística que las pruebas no paramétricas. Por lo tanto, es más probable detectar un efecto significativo cuando realmente existe uno. De modo que, con ello, puedes lograr aumentar la potencia estadística.
¿Cómo escoger la prueba paramétrica adecuada?
Existe una serie de criterios para saber cuándo podemos utilizar una prueba paramétrica y cuándo no, además de las condiciones de base arriba expuestas.
Según el número de muestras a comparar
La mayoría de personas que se dedican a la estadística suelen estar más familiarizadas con las pruebas paramétricas y, (por lo tanto con el análisis paramétrico) que con las no paramétricas. De todas formas, aquí hablaremos de las pruebas paramétricas para comparar dos o más muestras y de los criterios a considerar, que vienen marcados por el número de muestras, precisamente. A continuación se presentan algunas consideraciones a tener en cuenta:
En general, cuando se comparan dos muestras, la prueba t de Student es la prueba paramétrica más adecuada si se cumplen los supuestos. Si se comparan más de dos muestras, el ANOVA es una opción adecuada si se cumplen los supuestos. Si se desea controlar el efecto de una o más covariables, se puede utilizar ANCOVA o MANCOVA según el número de variables dependientes. Fíjate bien:
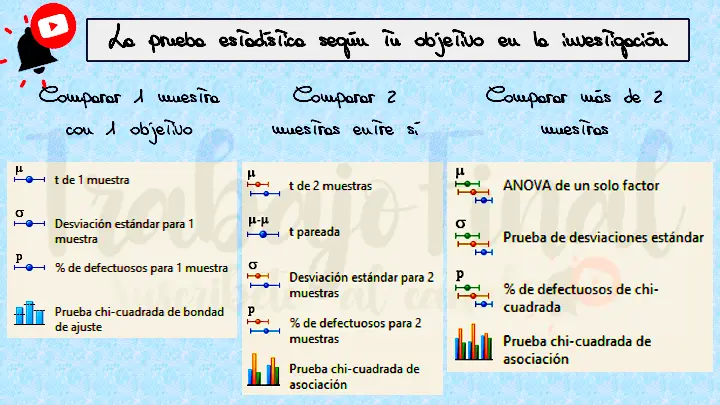

Según tipo de variable y de muestra
Existe una tabla comparativa que representa fácilmente qué tipo de prueba paramétrica podrías utilizar en caso de tratarse de:
- Una variable cualitativa versus una variable cuantitativa.
- Una muestra independiente versus relacionada.
| Tipo de variable | Muestras independientes | Muestras relacionadas |
|---|---|---|
| Cualitativa | Prueba Z de comparación de proporciones | Test de Mc Nemar |
| Cualitativa | X2 de Pearson | |
| Cualitativa (k=2) | t de Student-Fisher | t de Student- Fisher |
| Cualitativa | Análisis de la varianza | Wilcoxon |
| Cuantitativa | U de Mann-Whitney | |
| Cualitativa (k>2) | Análisis de la varianza | Análisis de la varianza |
| Cuantitativa | Kruskal-Wallis | Friedman |
Aplicar una prueba o un análisis de tipo paramétrico supone una serie de ventajas e inconvenientes que debes valorar.
Ventajas e inconvenientes de las pruebas paramétricas
A continuación las ventajas y los inconvenientes de aplicar las pruebas paramétricas en una investigación.
Ventajas
Si bien es cierto que no siempre podrás utilizar una prueba paramétrica, cuando se cumplen todos los requisitos y procedes a aplicarla en tu estudio, vas a obtener una serie de ventajas que son incomparables con las que aportan las pruebas no paramétricas. Por ejemplo, tienen más poder de eficiencia, son más sensibles a los rasgos de los datos recolectados, hay menor probabilidad de errores y dan estimaciones probabilísticas bastante exactas. Sin embargo, esto es sólo una parte de las ventajas.
Te dejo con todas las ventajas del uso de la prueba paramétrica:
- Mayor Potencia Estadística: Las pruebas paramétricas suelen ser más potentes que las no paramétricas, lo que significa que tienen una mayor probabilidad de detectar una verdadera diferencia o relación cuando existe, dado un tamaño de muestra específico.
- Uso de la Información Completa de los Datos: Las pruebas paramétricas toman en cuenta la magnitud y la variabilidad de los datos, proporcionando una utilización completa de la información contenida en los datos. Esto puede resultar en una mayor precisión en las estimaciones y en las pruebas de hipótesis.
- Requisitos de Tamaño de Muestra Flexibles: Aunque las pruebas paramétricas tienen supuestos sobre la distribución de los datos (normalmente, normalidad), con tamaños de muestra grandes. El Teorema del Límite Central sugiere que las medias de las muestras se distribuirán normalmente independientemente de la forma de la distribución de la población. Esto hace que las pruebas paramétricas sean aplicables en una gama más amplia de situaciones.
- Manejo de Datos Asimétricos y No Normales: Con tamaños de muestra adecuadamente grandes, las pruebas paramétricas pueden manejar ciertas desviaciones de la normalidad, aunque los datos sean ligeramente asimétricos o no normales.
- Control de Dispersión Diferente: Las pruebas paramétricas ofrecen procedimientos para ajustar las diferencias en la dispersión o varianza a través de los grupos, como Welch’s t-test, que no asume homogeneidad de varianzas.
- Efectos de Tamaño y Estimaciones de Intervalo de Confianza: Las pruebas paramétricas proporcionan efectos de tamaño e intervalos de confianza que pueden ser más interpretables y útiles en el contexto de la investigación.
- Aplicación Amplia en Software Estadístico: Las pruebas paramétricas son ampliamente soportadas y documentadas en la mayoría de los paquetes estadísticos, lo que facilita su aplicación y la interpretación de los resultados.
En definitiva:
Es decir, que tiene mayor capacidad para conducir a un rechazo de H0. La mayoría de las veces, el valor p asociado a una prueba paramétrica es menor que el valor p asociado a su equivalente no paramétrica ejecutada sobre los mismos datos.
Desventajas
No podemos ignorar que, igual que ofrecen millones de ventajas, también suponen ciertos riesgos a la hora de usarlas. Riesgos o desventajas:
- Las pruebas paramétricas son más complicadas de calcular.
- Presentan limitaciones en los tipos de datos que se pueden evaluar.
- Se ven afectadas por los valores atípicos como los datos ordinales.
Entonces, ¿Cuál es la mejor prueba paramétrica?
Ya te lo dije al principio, no hay una mejor prueba paramétrica que otra. Debes tener en cuenta las condiciones de validez que deben cumplirse según el caso, para que el resultado de aplicar la prueba paramétrica sea fiable.
De manera que la prueba t de Student para dos muestras independientes será fiable solo si cada muestra se ajusta a una distribución normal y si las varianzas son homogéneas.
Mientras que el ANOVA de un factor (One-Way ANOVA) requiere que todas las categorías o grupos bajo estudio no solo cumplan con la suposición de normalidad, sino también que compartan varianzas similares entre sí para garantizar comparaciones justas de sus medias. Además, para aplicar correctamente estas pruebas, es esencial que las muestras sean independientes unas de otras, lo que significa que la selección o los resultados de una muestra no deben influir en la selección o resultados de otra.
En el caso de pruebas más complejas, como el ANOVA de medidas repetidas o el MANOVA, además de las condiciones ya mencionadas, se introducen suposiciones adicionales. Por ejemplo, en el ANOVA de medidas repetidas, se asume la esfericidad, que implica que las varianzas de las diferencias entre todas las combinaciones posibles de pares de grupos son iguales. Esta condición es crucial para la validez de los tests F que se utilizan para determinar la significancia estadística de las diferencias observadas.
Por otro lado, el MANOVA, al tratar con múltiples variables dependientes, no solo requiere la verificación de la normalidad multivariante, sino también la igualdad de las matrices de covarianza (homogeneidad de covarianzas) entre los grupos.
Cada una de estas pruebas paramétricas está diseñada para situaciones específicas y ofrece ventajas únicas cuando se aplican correctamente. Sin embargo, la validez de sus resultados descansa en el cumplimiento riguroso de sus respectivos supuestos. Cuando estos supuestos no se cumplen, los investigadores pueden recurrir a transformaciones de los datos para satisfacer los requisitos de normalidad y homogeneidad de varianzas, o considerar el uso de pruebas no paramétricas, las cuales son menos estrictas en cuanto a las condiciones de los datos, pero pueden ofrecer menos poder estadístico para detectar diferencias significativas.
Resumen
Las pruebas paramétricas más recurrentes en los TFG de Psicología son la prueba T de Student, la ANOVA, la ANCOVA y la prueba MANCOVA.
- Prueba t de Student: Apropiada para comparar dos muestras independientes, con tamaños de muestra pequeños (menos de 30) y distribuciones normales o aproximadamente normales.
- Prueba ANOVA: Utilizado para comparar más de dos muestras independientes, con tamaños de muestra pequeños o grandes, y distribuciones normales o aproximadamente normales.
- Prueba ANCOVA: Una extensión del ANOVA que se utiliza para comparar más de dos muestras independientes, teniendo en cuenta una o más covariables continuas.
- Prueba MANCOVA: Apropiado para comparar más de dos muestras independientes en múltiples variables dependientes continuas, teniendo en cuenta una o más covariables continuas.
