En la entrada en la que te expongo las diferentes formas de identificar el tipo de análisis que puede necesitar tu investigación según el número de variables y tus necesidades, te planteaba que era importante valorar si lo que estabas comparando en el pre-post test de tu intervención se acogía más a un modelo de medias o de medianas en cuestión de resultados.
Aquí te hago un resumen rápido para repasar contenidos al respecto de estos dos conceptos, sumando un tercero: la moda. Estamos hablando de las medidas de tendencia central más utilizadas: la media, mediana y moda. Que distan completamente de las medidas de dispersión que abordaremos en otra entrada.
¿Qué son las medidas de tendencia central?
Las medidas de tendencia central son medidas estadísticas que buscan acotar o resumir todo un conjunto de valores en uno solo. Representan una referencia central, en torno al cual se encuentra ubicado el conjunto de los datos. Estas medidas son, principalmente, tres: la media, la mediana y la moda, y pretenden medir el grado de concordancia entre los datos de la variable. Por otro lado, están las medidas de dispersión con las que se evalúa el grado de dispersión de los valores de una (univariable) o varias variables (multivariable). Con este segundo tipo de medidas, se pretende determinar en qué grado los datos difieren los unos de los otros.
El criterio general para determinar qué tipo de procedimiento estadístico para valorar la posición o la dispersión va a depender del tipo de organización o de ordenación que tengan los datos. Si los datos se encuentran ordenados en una tabla estadística diremos que se encuentran “agrupados” y si los datos no están en una tabla hablaremos de datos “no agrupados”. A continuación, definiremos y pondremos un ejemplo explicativo en cada caso para entender en qué consisten las medidas de tendencia central principales, concretamente: la media, la mediana y la moda.
La media y un ejemplo
Dado un conjunto de datos, la media es la suma de todos los datos dividida entre la cantidad de datos (n) y, normalmente, se representa con la siguiente fórmula:


Aunque también puedes encontrar la siguiente fórmula:


De manera que, por ejemplo, si tenemos 4 notas en una asignatura que hacen alusión a los resultados de los exámenes de ésta con un peso del 25% de la nota final de una asignatura, se trataría de sumar las cuatro evaluaciones y dividir el resultado por cuatro. En caso de no ser una media aritmética estaríamos ante una media ponderada, que daría diferente peso a los valores hasta sumar el 100%.
La media ponderada es una medida de tendencia central, que es apropiada cuando en un conjunto de datos cada uno de ellos tiene una importancia relativa respecto de los demás datos.
La media aritmética (no ponderada) se representa con una linea horizontal sobre una Y como en la fórmula, aunque también puede usarse una X (x̄):


De manera que, por ejemplo, si tenemos un 7, un 6, un 8 y un 5 y queremos calcular el promedio o, lo que es lo mismo, el resultado final en la asignatura, entonces: 7 + 6 + 8 + 5 = ?
La media aritmética o promedio es 26/4 = 6,5 de nota final en la asignatura.
La desviación, en este punto, viene dada por la diferencia entre el valor del dato y la media. Por ejemplo, partiendo de la media (6.5), obtendremos las siguientes desviaciones, para cada caso:
| Calificaciones | Desviación |
|---|---|
| 7 | 7-6.5=0.5 |
| 6 | 6-6.5=-0.5 |
| 8 | 8-6.5=1.5 |
| 5 | 5-6.5=-1.5 |


Mediana y ejemplo
La mediana es el dato que ocupa una posición central y para averiguarlo, debemos ordenar los datos primeramente (de menor a mayor, por ejemplo).
- Si hay un número impar de datos, la mediana es el dato de la posición n+12n+12.
- Si hay un número par de datos, la mediana es la media de los dos datos centrales, es decir, la media de los datos de las posiciones n/2n/2 y n/2+1n/2+1.
Se dice que la mediana, la media y la “varianza” son valores estadísticos muy ilustrativos de una distribución. La media puede estar “desplazada” hacia un lado o hacia otro de dicha distribución de datos. Pero la mediana siempre se sitúa en el “centro” de dicha distribución.
Moda y ejemplo
La moda es el dato que más se repite. En este sentido, puede haber más de una moda si hay varios datos que se repiten el mismo número de veces (multimodal) y puede no haber moda si ningún dato se repite. Por ejemplo, tenemos que el número de hermanos de un grupo de 5 participantes es 1, 3, 0, 2 y 2, tal que así:
| #Participante | Número de hermanos que tiene cada sujeto |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 0 |
| 4 | 2 |
| 5 | 2 |
Procedemos a calcular la media, llegando a la conclusión de que la media es de 1.6 hermanos; siendo, la moda, 2 (porque es el valor que más se ha repetido).
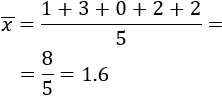
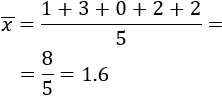
Moda unimodal
La moda del conjunto es 5 porque ha habido 2 repeticiones.


Moda bimodal
El máximo número de repeticiones se da para dos números. La moda del conjunto es 5 y 8 porque ambos números se repiten en dos ocasiones, mientras que el resto de números se repiten únicamente una vez.


Moda multimodal
El máximo número de repeticiones se da para tres o más números. La moda del conjunto son tres números: 3, 5, 8 que se repiten la misma cantidad de veces.


Conclusiones sobre la media, la mediana y la moda
Ya hemos visto que la media, la mediana y la moda son medidas de tendencia central, sin embargo, hacen alusión a conceptos bien diferenciados. Es más, podemos asumir que existen claras diferencias entre la media, la mediana y la moda al respecto de: su utilidad, la forma de calcular y, al fin y al cabo, en su definición. A continuación te presento una tabla comparativa en la cual podrás valorar los puntos clave más importantes que hemos abordado en esta entrada.
| Media | Mediana | Moda | |
|---|---|---|---|
| Definición | El valor obtenido al sumar todos los datos (sumatorio) y dividir el resultado entre el número total de datos. | El valor numérico que separa la mitad superior de un conjunto de la mitad inferior. | El valor numérico más veces votado o escogido por la razón que sea. |
| Promedio o media aritmética de un conjunto. | Indica la posición central. | Indica el valor que más se repite. | |
| Cuándo es útil | La media se utiliza para distribuciones normales de números, con una cantidad baja de valores atípicos. | La mediana se usa, por lo general, cuando queremos devolver la tendencia central en el caso de distribuciones numéricas sesgadas. | Cuando queremos contabilizar cuál es la opción más votada o escogida por un grupo de sujetos. |
| Forma de calcular | La media se calcula sumando todos los valores y dividiendo la suma entre el número total de valores. | Se puede calcular poniendo los números en orden ascendente y luego localizando el número del centro de esa distribución. | Se hayan los valores más repetidos en una secuencia o conjunto. |
| Ejemplo de distribución normal | 2, 3, 3, 5, 8, 10, 11= (2+3+3+5+8+10+11)/7= 6. Es decir, la media es 6 | 2, 3, 3, 5, 8, 10, 11. Es decir, la mediana es 5 | 2, 3, 3, 5, 8, 10, 11. La moda es 3. |
| Ejemplo de uso | Tenemos los resultados de varios exámenes en una asignatura y queremos calcular la nota media que sale para saber si hemos aprobado o no. | La mediana podría ser aplicada al ámbito educativo para valorar la nota de corte para aprobar en base a la distribución de los resultados obtenidos en un aula tras la realización de un examen de «selectividad». | La moda puede ejemplificarse por las votaciones que tienen lugar entre un grupo de personas que quiere llegar a un acuerdo. |
Representación gráfica de moda, mediana y media
A continuación, dispones de una comparativa de la representación gráfica de las tres medidas de tendencia central explicadas: moda, mediana y media.






Puede pasar que una media distorsione la realidad, bien porque haya datos muy dispares o por la existencia de valores atípicos. Es, precisamente, con la expresión de «distribución numérica sesgada«, que nos estamos refiriendo a la existencia de estos valores atípicos que podrían poner en riesgo la relación entre las variables observadas. Puedes leer con mayor profundidad sobre esto en la entrada dedicada a los valores atípicos.
Conclusiones
A modo de conclusión, te ofrezco el siguiente video explicativo. Porque hay diferentes maneras de aprender y la audiovisual no iba a ser menos:
Otros conceptos importantes en estadística
Las pruebas paramétricas.
Ventajas e inconvenientes del uso de una prueba paramétrica o no paramétrica.
